第1回:マンデルブロ集合を計算してみる - 超ウィザード級ハッカーのたのしみ
第2回:マンデルブロ集合を計算してみる2 - 超ウィザード級ハッカーのたのしみ
第3回:マンデルブロ集合を計算してみる3 - 超ウィザード級ハッカーのたのしみ
マンデルブロ集合に含まれるcに対して、以下の漸化式がどういう振る舞いをするかが気になっています。
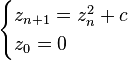
cが実数の場合は、ただのロジスティック写像なので既にアホみたいに調べられています。以下は分岐図と呼ばれるものです。プロットがあるところに値が収束します。値が複数あるときは、複数の値を繰り返す動きに収束します。

マンデルブロ集合の絵と比較すると面白いことがわかります。

右から順に。
分岐図が1本のところは絵のアの領域に相当します。ここでは1つの値にzが収束していきます。おそらく、このハート型の上の点ではzが周期1の固定点に収束するでしょう。
分岐図が2本のところは絵のイの領域です。この島は周期2で2つの値が交互に現れるようにzが収束していくものと思われれます。z=0となるc=-1もこの島に含まれています。
さらに左にいって、分岐が4本になったところにはウの領域です。この島ではzは周期4で値を繰り返すようになるようです。
エの小さい島では、分岐が8本になります。
エ・オ・カ・キの島の間、あるいは先の棒では値が一定しない、いわゆるカオスとなります。
オ・カ・キの島のがあるところでは、分岐図の値が分散していません。バンドと呼ばれる領域です。
どうやら、マンデルブロ集合の島は、zの振る舞いと関連しているらしいです。