前々回:マンデルブロ集合を計算してみる - 超ウィザード級ハッカーのたのしみ
前回:マンデルブロ集合を計算してみる2 - 超ウィザード級ハッカーのたのしみ
マンデルブロ集合は以下示される複素数列の挙動について表したものである。
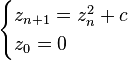
そこで、この複素数列z_nの動きを絵にしてみました。画像の各点が複素数cのときのz_nを表しています。横軸がcの実部を変えたとき、縦軸がcの虚部を変えたときを示しています。複素数z_nの偏角を色相で表し、絶対値を明度で表します。絶対値が大きいと明度が小さくなる、つまり黒色になります。
n=1
色相が不連続な点はz_1=0の点を示しています。c=(0,0)(複素数a+biを(a,b)と表します)の点でz_1=0となります。
z_1=0というのはz_nが初期値z_0=0に戻ったことを意味しています。c=(0,0)の点では、周期1の繰り返し、つまり全てのnでz_nは同じ値となります。

n=2
c=(0,0)の点で、z_2=0です。以下のどのnの絵でもc=(0,0)の点では色相が不連続です。
別の色相が不連続な点があります。c=(-1,0)の点です。この点は2ステップでz_nが初期値に戻る、つまり周期2でz_nの値が繰り返します。

n=3
周期1と周期3で繰り返す点で色相が不連続になっています。周期3の点が3つあることがわかります。n=3までのz_n=0となる点は手で計算可能です。

n=4
周期が1,2,4で繰り返す点で色相が不連続になっています。z_nが発散してきた点は黒で表示されています。

n=11
以降同様になりますが、適当に3例だけ貼っておきます。

n=47
素数の場合はz_n=0の点は少なくなります。

n=720
逆にn=6!=720のように約数の多い数はz_n=0の点も多くなります。

考え事
マンデルブロ集合の定義から、マンデルブロ集合には、全ての自然数の周期でz_nが繰り返す点が含まれています。この点の集合をAとします。*1
マンデルブロ集合と集合Aは一致するのでしょうか?おそらく一致しないと予想します。
その場合に、マンデルブロ集合に含まれて、集合Aに含まれない点はどういう動きをするのでしょうか?*2ある値の近傍をぐるぐる回るような動きをするような気がします。もしかしたら、どこかの値に漸近していくやつもいるかもしれません。
また、マンデルブロ集合と集合Aは濃度的な意味でどちらが多いのでしょうか?*3
マンデルブロ集合のフチの集合は、全て集合Aに含まれないのか、全て集合Aに含まれるのか?一部だけ含まれるというのはなさそうです。*4少なくとも、マンデルブロ集合の中の集合に、集合Aの一部は含まれているようです。