クラスの依存関係グラフ 3
Java および Scala のクラスの依存関係のグラフについて調べている。
驚くべきことに(まあ予想はしていたけれども)、クラス間の依存関係のグラフはスケールフリーネットワークの性質を持つことが明らかになりました。スケールフリーネットワークでは、ノードの次数がべき乗則に従います。
勉強しながら調べているので、次数の非常に大きいクラス、例えば java.lang.Object クラスの存在がべき乗則で現れうるクラスなのかべき乗則でも説明できないほど例外的に次数の大きいクラスか、よくわからないと前回・前々回に素人っぽい言及をしました。
プロットの仕方を工夫すると、次数が大きいところも綺麗に図がかけることがわかったので、今回は次数が大きいところでもべき乗則が成立しているかどうかを検証します。
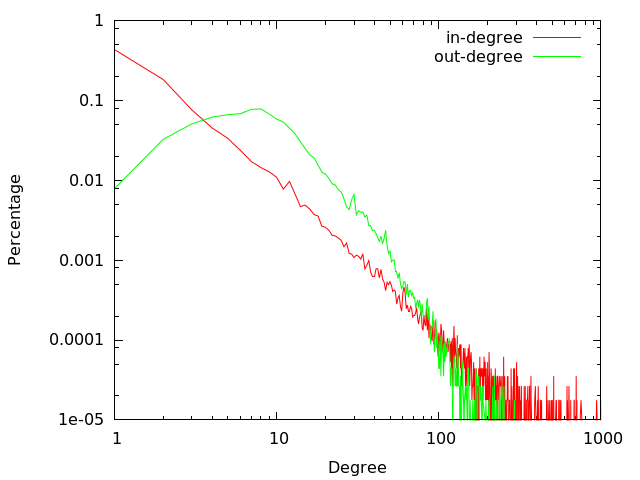
上は前回載せた図で、次数の分布を示しています。これは、Bin の幅が 1 のヒストグラムです。次数が大きいところはサンプルが少ないのでガタガタになっていてべき乗則なのかどうかよく分からなくなっています。
そこで、Bin の幅を 1 に固定せずに、対数プロットしたときに Bin の幅が同じにやるようなヒストグラムを書きます。つまり、1 つめの Bin は次数が 1 のノードの割合、2 つめの Bin は次数が 2 か 3 のノードの値、3 つめは 4, 5, 6, 7 のいずれか、N つめは log2(N-1) から log2(N)-1 となります。
上のような Log-Bin で書いたヒストグラムが下の図です。

次数が高いところは前の図ではが省きました、Log-Bin で描くと次数が高いところまでグラフに含められるようになりました。
入力次数は、次数が大きいところまで、きれいなべき分布になっていることが分かります。次数が 10^5 といった非常に大きな値を持つノードは、java.lang.Object クラスなのですが、この存在もべき乗則に従うことが分かりました。
出力次数は、次数が小さいところはよくわからない分布をしていますが、次数が大きいとべき乗則っぽい分布になっています。
累積分布を描いても、次数の高いところが上手く表現できます。
下の2つの図は、次数 k に対して、次数が k を超えるノードの割合を示しています。上の図が入力次数、下の図が出力次数です。*1

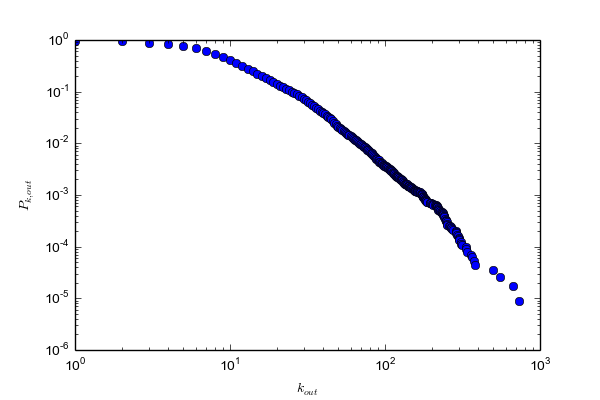
Log-Bin だとプロットの数が減るのでデータが丸められてしまっている不安がありますが、累積分布ではプロットの数は減りません。
さて、入力次数の方に関しては、きれいなべき乗則になっています。グラフの傾きは -1 です。累積分布の場合は傾きは べき指数 + 1 になります。累積なのに、k が小さいところの P が 1 になっていませんが、それは k = 0 のノードがいるからです。また、ヒストグラムを描いたときには気付かなかったが、次数が 10 以下のところで傾きが少し緩くなっています。べき乗則に従うと言われるデータは一般的にこうなっています。次数が大きいところはちょっとガタガタっとなっていますが、k = 10^4 に何か意味があるとは思えないので、ノイズでしょう。
出力次数の方が、k = 30 から k = 200 まではべき乗則に従っています。k が小さいところは謎の分布なのは、Log-Bin の図の方が分かりやすいです。
出力次数の次数が大きいところは、ガタガタしてわかりづらいが、グラフの傾きが急になっているようにも見えます。ソフトウェアを作る視点で考えると、出力次数は、ソースコードを書く人間が決めることで、あまりに依存先が多いクラスというのは作らないものなので、上限値があることが予想されます。べき乗則に従うということはサンプル数を増やせば、想像を絶する巨大なクラスが現れるということを意味していますが、おそらくありえないでしょう。10^3 のオーダーが上限なのではないかと推測されます。このことに関しては、ソフトウェア特有の現象なので、もう少し調べる価値がありそうです。
今はべき指数は目分量で見ているので、次回は定量的にべき指数を計算してみようと思う。
参考

- 作者: Albert-László Barabási
- 出版社/メーカー: Cambridge University Press
- 発売日: 2016/07/21
- メディア: ハードカバー
- この商品を含むブログを見る