KdV方程式を数値的に解いてみた。*1
KdV方程式は、以下の式で表される方程式です。

非線形の偏微分方程式だけれども、手計算で頑張ることができて、よく研究されてきた方程式です。バーガース方程式と同様の非線形項に加えて、3回微分の項がある。この項は分散項と呼ばれている。
これを解いてみて、Zabusky と Kruskal による有名な報告と同じ結果が得られることを確認した。
コードは記事の最後に載せる。PythonでNumPyを使った。NumPyは計算が早く、forループもなくなるので良いと思った。
空間の離散化には「擬スペクトル法」を用いた。擬スペクトル法というのは実空間と波数空間を行ったり来たりして、微分値を求める方法である。時間積分は4次の「ルンゲクッタ法」を使った。これは有名ですね。
つまり、無意味に高精度な計算をしている。
Zabusky と Kruskalが見つけたように、δ = 0.022のときに面白い動きをする。YouTubeに動画を上げた。
初期値にはcos波を与える。
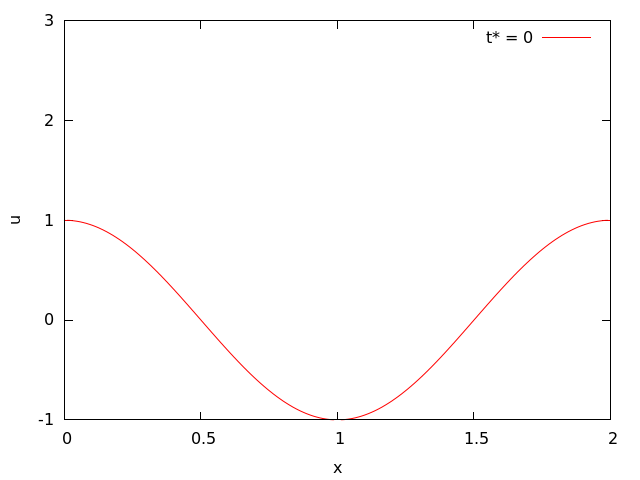
非線形項のために波が切り立って来る。

波の先が崩れる。

小さい波に別れる。

伝播していく。

波が重なりあうが、合体せずにいるようになる。

この小さい波は「ソリトン」といって、かなり前に物理学界で流行ったらしい。動画を見ていると、いかにも力学的に意味がありげな動きをしていて面白い。
*1:先日の計算が誤っていたので再投稿